如何使用三行代码将模型训练速度提高 2 倍
您是否曾希望您的深度学习模型能够运行得更快?
GPU 价格昂贵。数据集非常庞大,训练过程似乎永无止境;您需要进行一百万次实验,并且有一个最后期限要满足 —— 所有这些都是期待特定形式的训练加速的充分理由。
但是该选择哪一个呢?
PyTorch、HuggingFace和Nvidia已经在模型训练的性能调整方面提供了很好的参考,包括异步数据加载、缓冲区检查点、分布式数据并行化和自动混合精度。
在本文中,我将介绍自动混合精度技术。我将首先简要介绍 Nvidia 的张量核心设计,然后介绍在 ICLR 2018 上发表的开创性工作“混合精度训练”论文,最后介绍在 FashionMNIST 上训练 ResNet50 的简单示例,以及如何在仅使用三行额外代码的情况下将训练速度提高 2 倍,同时加载 2 倍的批处理大小。

硬件基础知识——Nvidia Tensor Cores
首先,让我们回顾一下 GPU 设计的一些基本原理。Nvidia GPUS 最受欢迎的商业产品之一是 Volta 系列,例如基于 GV100 GPU 设计的 V100 GPU。因此,我们将围绕下面的 GV100 架构进行讨论。
对于 GV100,流式多处理器 (SM)是计算的核心设计。每个 GPU 包含 6 个 GPU 处理集群 (GPC) 和 S84 个 SM(对于 V100 则为 80 个 SM)。整体设计如下所示。

对于每个 SM,它包含两种类型的核心:CUDA 核心和 Tensor 核心。CUDA核心是 Nvidia 于 2006 年推出的原始设计,是 CUDA 平台的重要组成部分。CUDA 核心可分为三种类型:FP64 核心/单元、FP32 核心/单元和 Int32 核心/单元。每个 GV100 SM 包含 32 个 FP64 核心、64 个 FP32 核心和 64 个 Int32 核心。Volta /Turing (2017) 系列 GPU 引入了Tensor 核心,以区别于之前的 Pascal (2016) 系列。GV100 上的每个 SM 包含 8 个 Tensor 核心。此处提供了V100 GPU的完整详细信息列表。下面详细介绍了 SM 设计。
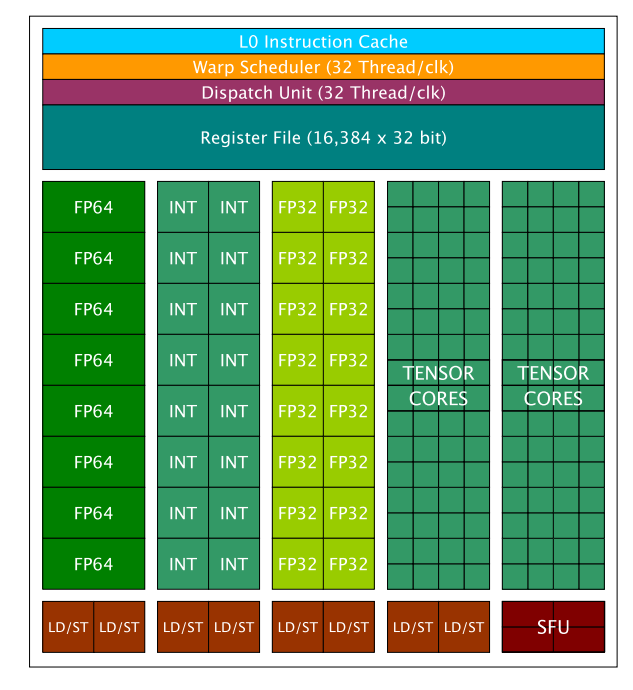
为什么要使用 Tensor 核心?Nvidia Tensor 核心专门用于执行通用矩阵乘法 (GEMM) 和半精度矩阵乘法和累加 (HMMA) 运算。简而言之,GEMM 以 A*B + C 的格式执行矩阵运算,而 HMMA 将运算转换为半精度格式。详细讨论可在此处找到。由于深度学习大量涉及 MMA,因此Tensor 核心在当今的模型训练和加速中至关重要。
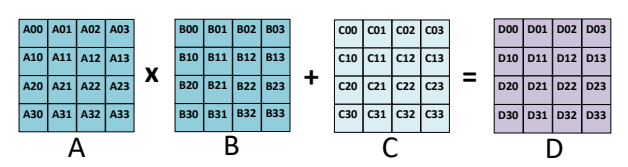
当然,在切换到混合精度训练时,请务必检查所用 GPU 的规格。只有最新的 GPU 系列才支持 Tensor 核心,并且只能在这些机器上使用混合精度训练。
数据格式基础知识 – 单精度(FP32)与半精度(FP16)
现在,让我们仔细看看 FP32 和 FP16 格式。FP32 和 FP16 是使用 32 位二进制存储和 16 位二进制存储表示浮点数的 IEEE 格式。两种格式都包含三部分:a) 符号位、b) 指数位和 c) 尾数位。FP32 和 FP16 在分配给指数和尾数的位数上有所不同,这导致不同的值范围和精度。
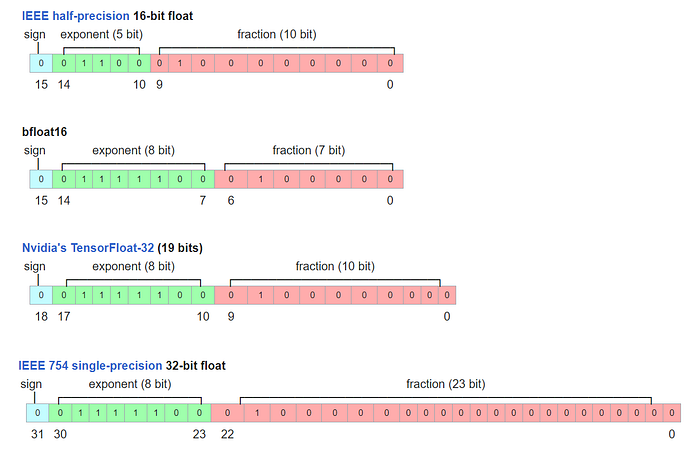
如何将 FP16 和 FP32 转换为实数?根据 IEEE-754 标准,FP32 的十进制值 = (-1)^(符号) × 2^(十进制指数 —127) × (隐式前导 1 + 十进制尾数),其中 127 是偏置指数值。对于 FP16,公式变为 (-1)^(符号) × 2^(十进制指数 — 15) × (隐式前导 1 + 十进制尾数),其中 15 是相应的偏置指数值。在此处查看偏置指数值的更多详细信息。
从这个意义上讲,FP32 的值范围约为 [-2¹²⁷, 2¹²⁷] ~[-1.7*1e38, 1.7*1e38],FP16 的值范围约为 [-2¹⁵, 2¹⁵]=[-32768, 32768]。请注意,FP32 的十进制指数介于 0 到 255 之间,我们排除了最大值 0xFF,因为它代表 NAN。这就是为什么最大的十进制指数是 254-127 = 127。类似的规则适用于 FP16。
对于精度,请注意指数和尾数都会影响精度限制(也称为非规范化,请参阅此处的详细讨论),因此 FP32 可以表示高达 2^(-23)*2^(-126)=2^(-149) 的精度,而 FP16 可以表示高达 2^(10)*2^(-14)=2^(-24) 的精度。
FP32 和 FP16 表示之间的差异带来了混合精度训练的关键问题,因为深度学习模型的不同层/操作对值范围和精度不敏感或敏感,需要分别处理。
混合精度训练
现在我们已经了解了 MMA 的硬件基础、Tensor 核心的概念以及 FP32 和 FP16 之间的主要区别,我们可以进一步讨论混合精度训练的细节。
混合精度训练的概念最早出现在 2018 年 ICLR 论文《混合精度训练》中,即在训练过程中将深度学习模型转换为半精度浮点数,而不会损失模型精度或修改超参数。如上所述,由于 FP32 和 FP16 之间的关键区别在于取值范围和精度,因此该论文详细讨论了FP16 导致梯度消失的原因以及如何通过损失缩放来解决这个问题。此外,该论文还提出了一些技巧,例如使用 FP32 主权重复制以及使用 FP32 进行特定操作(例如缩减和矢量点生成累积)。
损失缩放。论文给出了使用 FP32 精度训练 Multibox SSD 检测网络的示例,如下所示。如果不进行任何缩放,FP16 梯度的指数范围 ≥ 2^(-24),并且以下所有内容都将变为零,与 FP32 相比是不够的。但是,通过实验,只需将梯度缩放 2³=8 倍,就可以使半精度训练精度回到与 FP32 匹配的状态。从这个意义上讲,作者认为 [2^(-27), 2^(-24)] 之间的额外几个百分点的梯度在训练过程中仍然很重要,而 2^(-27) 以下的值并不重要。
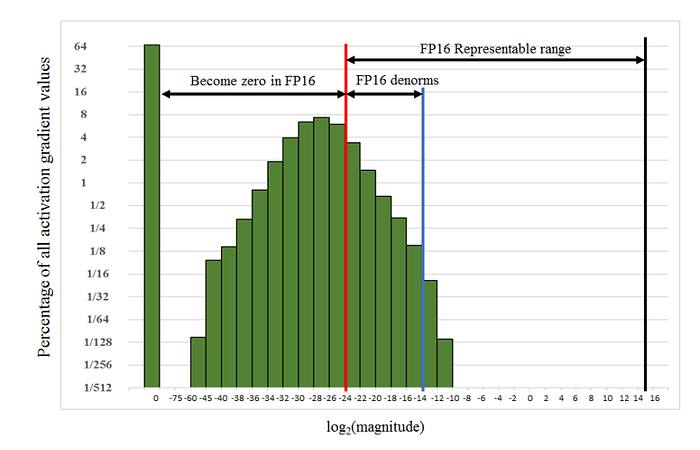
解决这种比例差异的方法是应用损失缩放。根据链规则,缩放损失将确保所有梯度都缩放相同的量。在最终权重更新之前,需要取消缩放梯度。
自动混合精度训练
Nvidia 最初将自动混合精度训练开发为 PyTorch 的扩展,称为 APEX,随后被 PyTorch、TensorFlow、MXNet 等主流框架广泛采用。请参阅此处的 Nvidia 文档。为简单起见,我们仅介绍 PyTorch 的自动混合精度库:https://pytorch.org/docs/stable/amp.html。
amp 库可以自动处理大多数混合精度训练技术,例如 FP32 主权重复制。用户主要接触ops autocast和梯度/损失缩放。
Ops autocast。虽然我们提到张量核可以大大提高 GEMM 操作的性能,但某些操作并不适合半精度表示。
amp 库给出了符合半精度要求的CUDA 操作列表。大多数矩阵乘法、卷积和线性激活都完全由 amp.autocast 覆盖,但是,对于减少/求和、softmax 和损失计算,计算仍然在 FP32 中执行,因为它们对数据范围和精度更敏感。
梯度/损失缩放。amp库提供了自动梯度缩放技术,因此用户无需在训练期间手动调整缩放。缩放因子的更详细算法可在此处找到。
一旦梯度被缩放,在梯度裁剪和正则化之前需要将其缩小。更多详细信息可在此处找到。
FashionMNIST 训练示例
torch.amp 库相对容易使用,只需要三行代码就可以将你的训练速度提高 2 倍。
我们从一个非常简单的任务开始,使用 FP32 在 FashionMNIST 数据集( MIT 许可证)上训练 ResNet50 模型;我们可以看到 10 个 epoch 的训练时间为 333 秒:
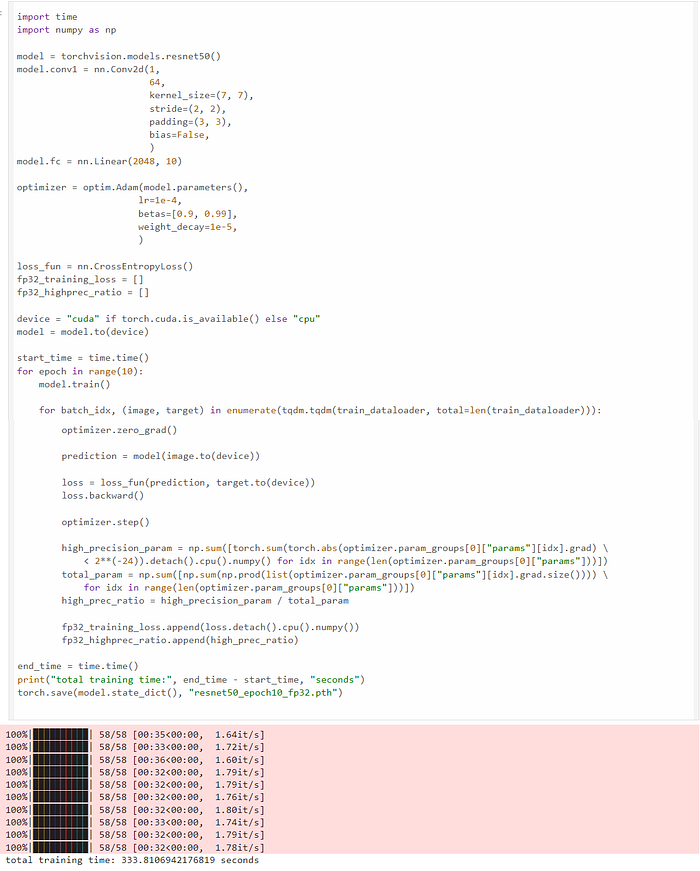
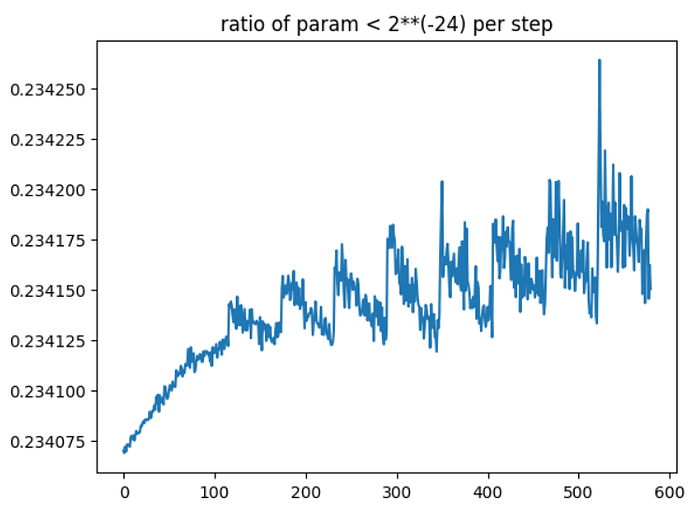
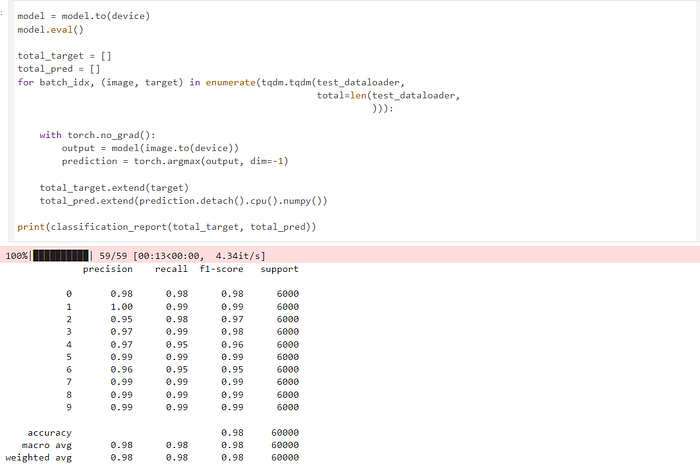
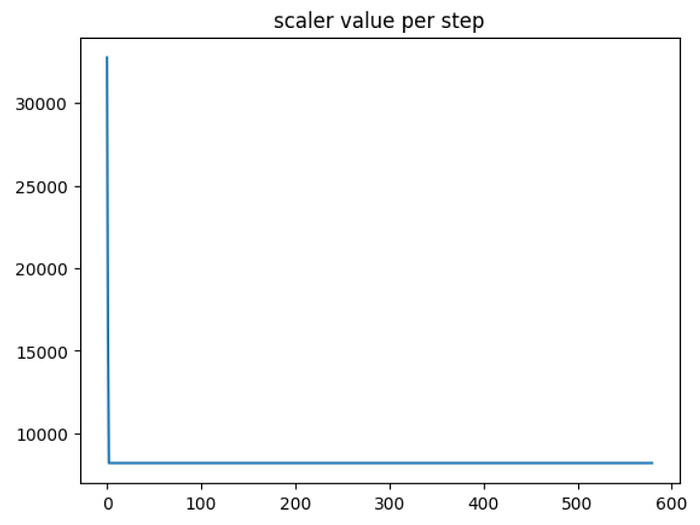
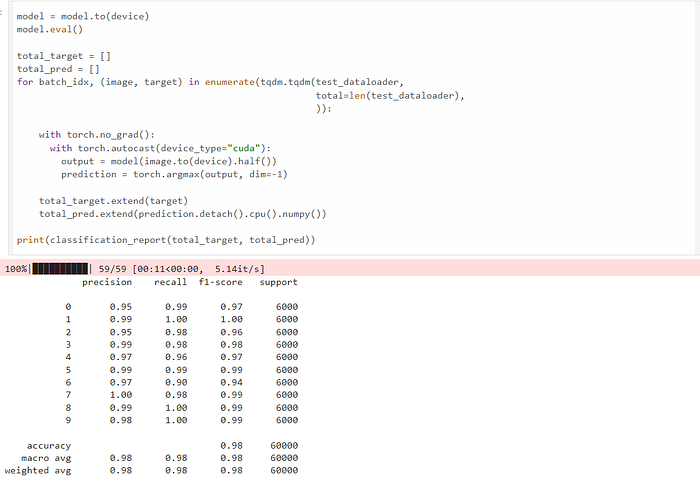
现在我们使用 amp 库。amp 库只需要三行额外的代码即可进行混合精度训练。我们可以看到训练在 141 秒内完成,比 FP32 训练快 2.36 倍,同时实现相同的精度、召回率和 F1 分数。
scaler = torch.cuda.amp.GradScaler()
# 开始你的训练代码
# ...
with torch.autocast(device_type= "cuda" ):
# 训练代码
# 包装损失和优化器
scaler.scale(loss).backward()
scaler.step(optimizer)
scaler.update()
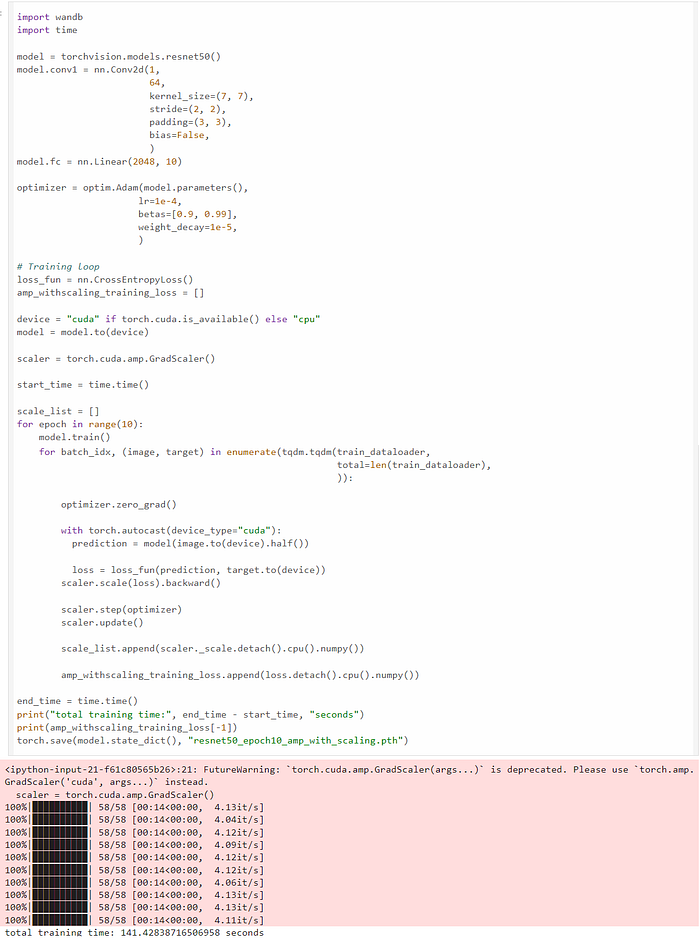
上面代码的 github 链接在这里。
概括
混合精度训练是加速深度学习模型训练的一项宝贵技术。它不仅可以加速浮点运算,还可以节省 GPU 内存,因为训练批次可以转换为 FP16,从而节省一半的 GPU 内存。使用 PyTorch 的 amp 库,额外的代码可以减少到三行,因为权重复制、损失缩放、操作类型转换都由库内部处理。
然而,如果模型权重大小远大于数据批次,混合精度训练并不能真正解决 GPU 内存问题。首先,只有模型的某些层被转换为 FP16,而其余层仍在 FP32 中计算;其次,权重更新需要 FP32 副本,这仍然占用大量 GPU 内存;第三,来自 Adam 等优化器的参数在训练期间占用大量 GPU 内存,而混合精度训练使优化器参数保持不变。从这个意义上讲,需要像 DeepSpeed 的 ZERO 算法这样的更先进的技术。
参考
- Micikevicius 等人,混合精度训练。ICLR 2018
- PyTorch AMP 库:https://pytorch.org/tutorials/recipes/recipes/amp_recipe.html
- Nvidia CUDA 浮点:https://docs.nvidia.com/cuda/floating-point/index.html